StructureNet: Hierarchical Graph Networks
for 3D Shape Generation
Kaichun Mo1*
Paul Guerrero2*
Li Yi1
Hao Su3
Peter Wonka4
Niloy J. Mitra2,5
Leonidas J.Guibas1,6
1Stanford University
2University College London
3University of California San Diego
4King Abdullah University of Science and Technology (KAUST)
5Adobe Research
6Facebook AI Research
*joint first authors
Siggraph Asia 2019
Abstract
The ability to generate novel, diverse, and realistic 3D shapes along with associated part semantics and structure is central to many applications requiring high-quality 3D assets or large volumes of realistic training data. A key challenge towards this goal is how to accommodate diverse shape, including both continuous deformations of parts as well as structural or discrete alterations which add to, remove from, or modify the shape constituents and compositional structure. Such object structure can typically be organized into a hierarchy of constituent object parts and relationships, represented as a hierarchy of n-ary graphs. We introduce StructureNet, a hierarchical graph network which (i) can directly encode shapes represented as such n-ary graphs; (ii) can be robustly trained on large and complex shape families; and (iii) be used to generate a great diversity of realistic structured shape geometries. Technically, we accomplish this by drawing inspiration from recent advances in graph neural networks to propose an order-invariant encoding of n-ary graphs, considering jointly both part geometry and inter-part relations during network training. We extensively evaluate the quality of the learned latent spaces for various shape families and show significant advantages over baseline and competing methods. The learned latent spaces enable several structure-aware geometry processing applications, including shape generation and interpolation, shape editing, or shape structure discovery directly from un-annotated images, point clouds, or partial scans.
Hierarchical Graph Network Architecture

Our variational autoencoder consists of two encoders and two decoders that both operate on our shape representation. The geometry encoder egeo encodes the geometry of a part into a fixed-length feature vector f, illustrated with a gray circle. The graph encoder egraph encodes the feature vectors of each part in a graph, and the relationships among parts, into a feature vector of the same size using graph convolutions. The graph encoder is applied recursively to obtain a feature vector z that encodes the entire shape. The reverse process is performed by the graph and geometry decoders d_graph and d_geo to reconstruct the shape. The decoder also recovers the geometry of non-leaf nodes.
Free Shape Generation

We show shapes in all categories decoded from random latent vectors, including shapes with bounding box geometry, and shapes with point cloud geometry. Parts are colored according to semantics, see the Supplementary for the full semantic hierarchy for each category. Since we explicitly encode shape structure in our latent representation, the generated shapes have a large variety of different structures.
Part Interpolation
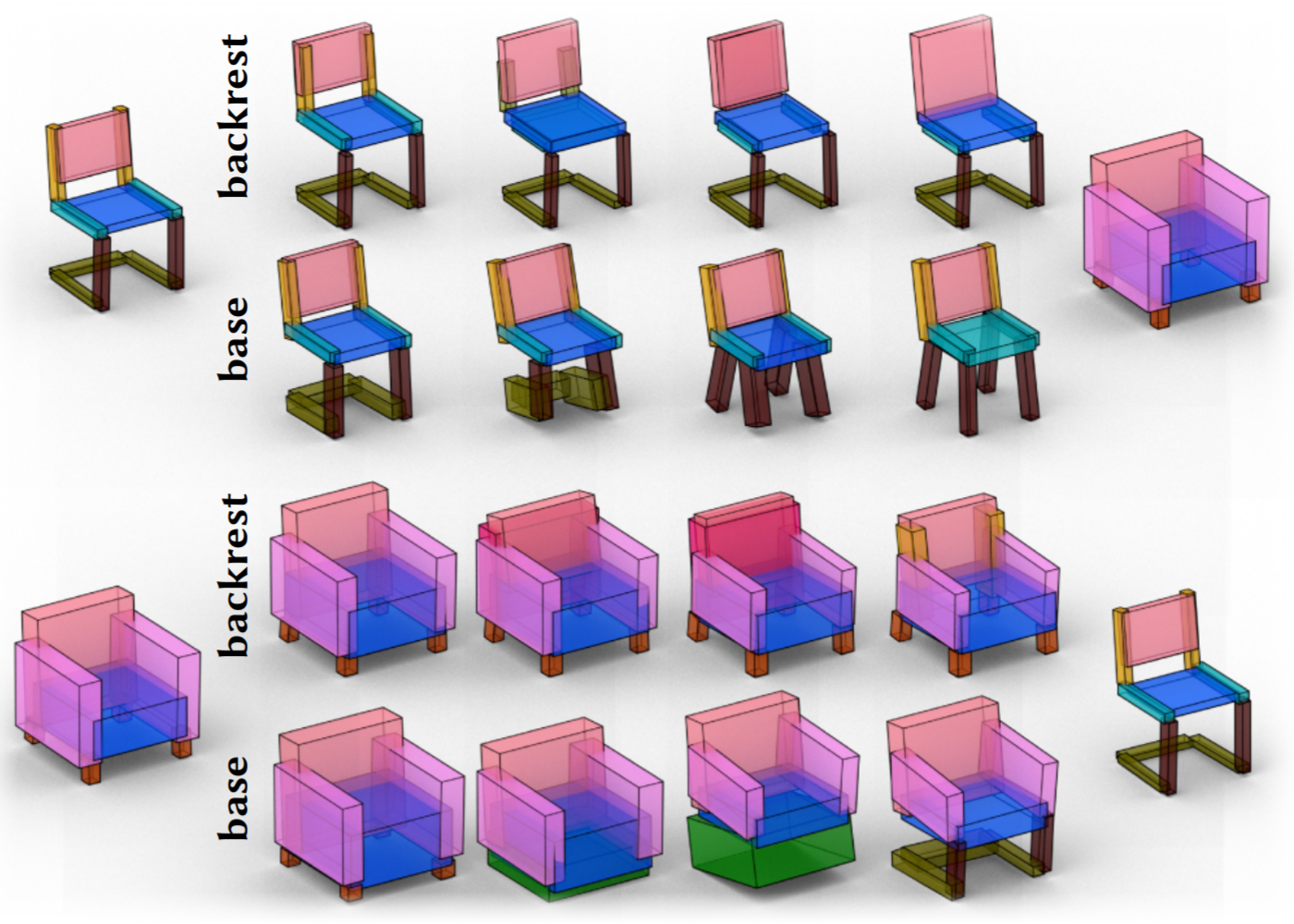
We interpolate either only the backrest (first row) or only the base (second row) between the chairs on the left and right side. Intermediate shapes preserve structural plausibility of the interpolated result mainly through geometric differences to the target part, but faithfully interpolate the structure. We observe that these interpolations are not necessarily symmetric: the base interpolations follow different paths to be compatible with the different back styles.
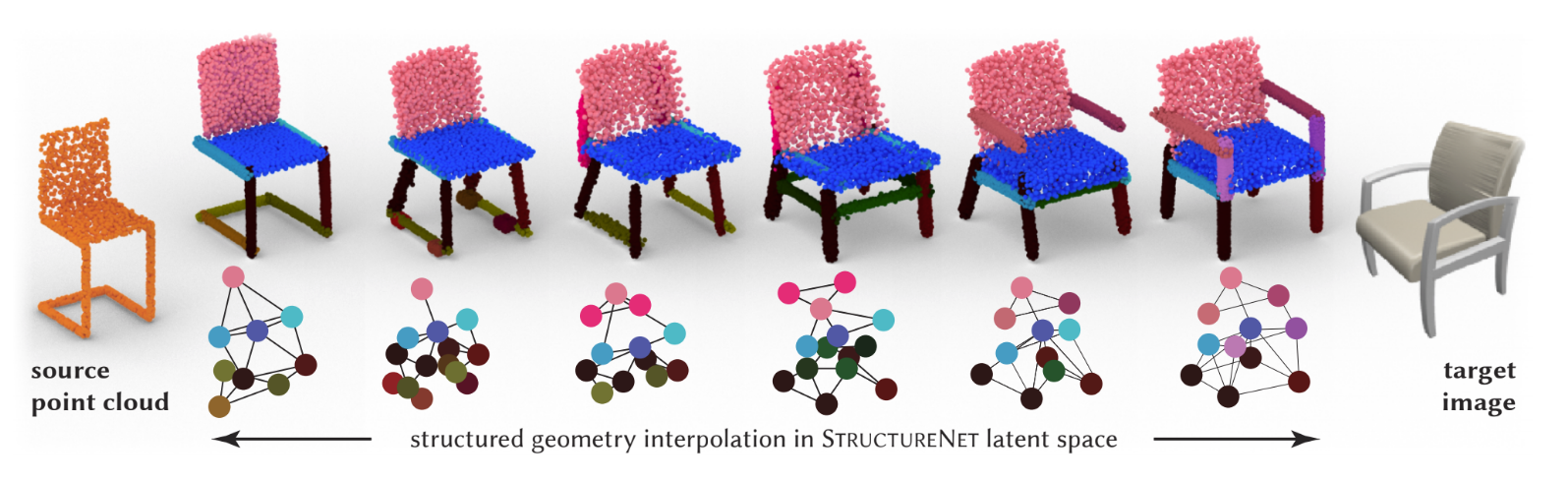
Shape Abstraction

Images, synthetic point clouds, and real-world scans from ScanNet [Dai et al. 2017] are embedded into our learned latent space, allowing us to effectively recover a full shape description that matches the raw input.
Structure-aware Shape Editing

We show editing results on two shapes with box geometry (first four rows) and two shapes with point cloud geometry (two bottom rows). For the two shapes with box geometry, we perform five different edits each, one edit per column. The edited box is highlighted in yellow, and the result is shown below. We see that the other boxes in the shape are adjusted to maintain shape plausibility. For the two shapes with point cloud geometry, we show intermediate results for one edit each. From left to right, these are (a) the original point cloud; (b) the predicted box abstraction; (c) the induced segmentation; (d) edited boxes; and (e) the induced edit of the point-cloud.
Bibtex
@article{MoGuerreroEtAl:StructureNet:SiggraphAsia:2019,
title={StructureNet: Hierarchical Graph Networks for 3D Shape Generation},
author={Mo, Kaichun and Guerrero, Paul and Yi, Li and Su, Hao and Wonka, Peter and Mitra, Niloy and Guibas, Leonidas},
journal={arXiv preprint arXiv:1908.00575},
year={2019}
}
Acknowledgements
This project was supported by a Vannevar Bush Faculty Fellowship, NSF grant RI-1764078, NSF grant CCF-1514305, a Google Research award, an ERC Starting Grant (SmartGeometry StG-2013-335373), ERC PoC Grant (SemanticCity), Google Faculty Awards, Google PhD Fellowships, Royal Society Advanced Newton Fellowship, KAUST OSR number CRG2017-3426 and gifts from Adobe, Autodesk and Qualcomm. We especially thank Kun Liu, Peilang Zhu, Yan Zhang, and Kai Xu for the help preparing binary symmetry hierarchies for GRASS baselines on PartNet. We also thank the anonymous reviewers for their fruitful suggestions.