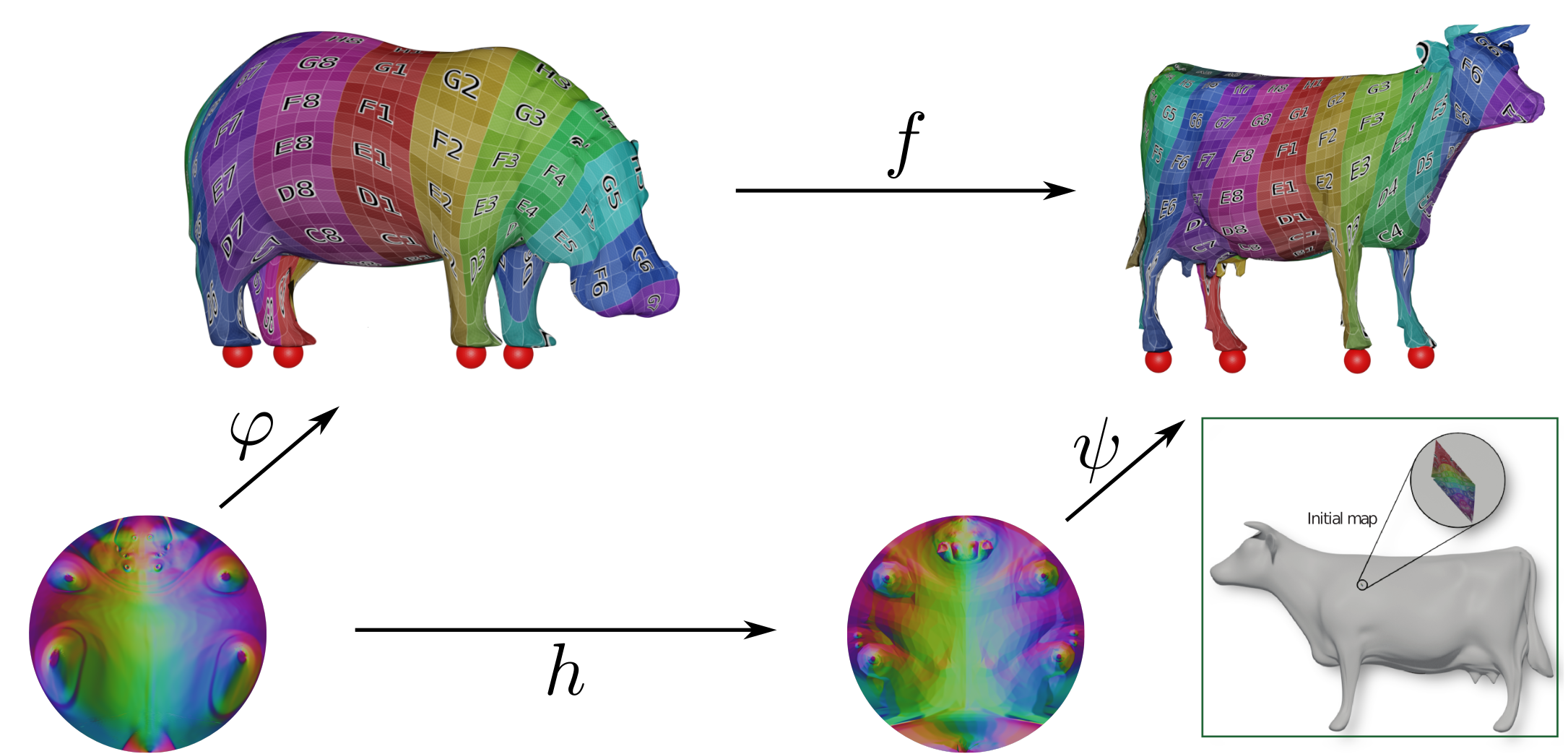
Neural surface maps are an alternative method to represent a surface map which hold two main advantages: differentiability and composability. Thanks to these properties, we compose multiple neural maps to define an inter-surface map that minimizes a differentiable distortion measure.

Abstract

Maps are arguably one of the most fundamental concepts used to define and operate on manifold surfaces indifferentiable geometry. Accordingly, in geometry processing, maps are ubiquitous and are used in many core applications, such as paramterization, shape analysis, remeshing, and deformation. Unfortunately, most computational representations of surface maps do not lend themselves to manipulation and optimization, usually entailing hard, discrete problems. While algorithms exist to solve these problems, they are problem-specific, and a general framework for surface maps is still in need.
We advocate considering neural networks as encoding surface maps. Since neural networks can be composed on one another and are differentiable, we show it is easy to use them to define surfaces via atlases, compose them for surface-to-surface mappings, and optimize differentiable objectives relating to them, such as any notion of distortion, in a trivial manner. In our experiments, we represent surfaces by generating a neural map that approximates a UV parameterization of a 3D model. Then, we compose this map with other neural maps which we optimize with respect to distortion measures. We show that our formulation enables trivial optimization of rather elusive mapping tasks, such as maps between a collection of surfaces.

Overfitting

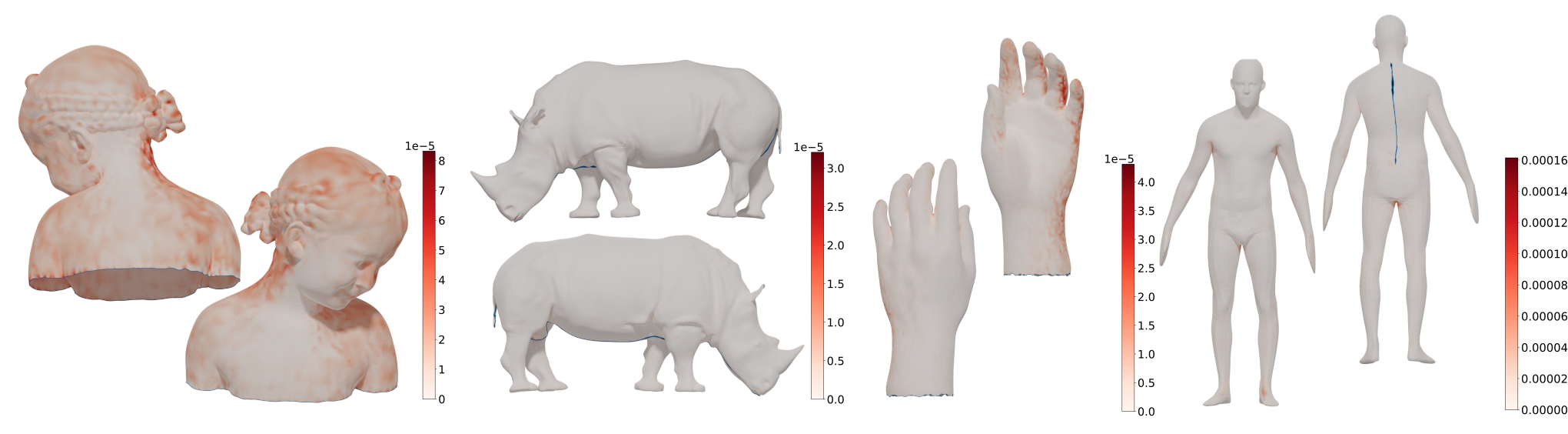
The figure above portrays neural surface maps for surfaces of diverse complexity. Colors highlight the point-wise euclidean error of our representation, while the corresponding color bars show the error scale.

Inter-surface Maps

Combining neural surface maps, we can achieve inter-surface maps with low distortion. The image shows an example of the evolution of surface to surface optimization between, in this case, Igea and David.

Collection Map

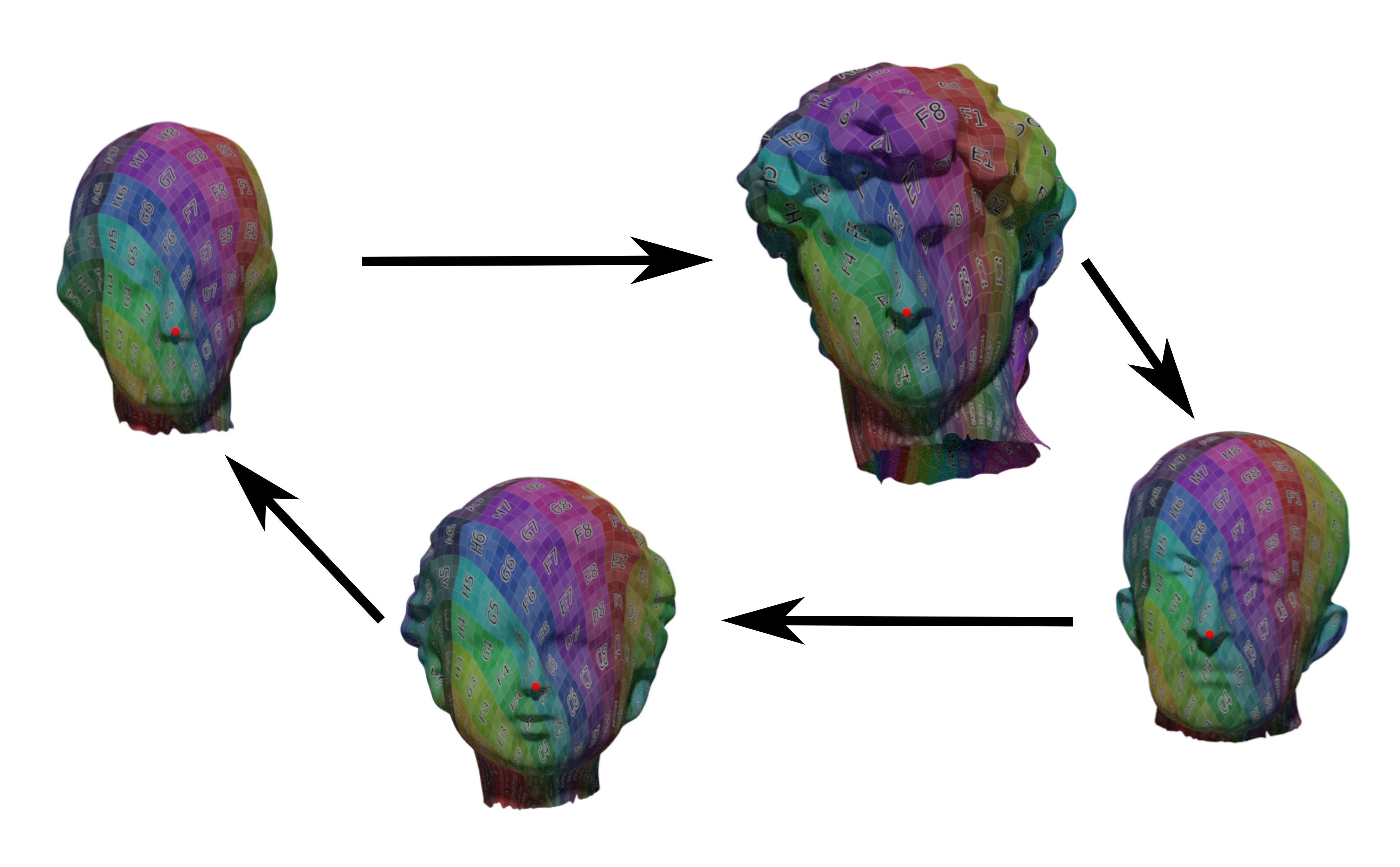
We map from one model to the other through a neural map. We then minimize the distortion between each different model. Cycle consistency is ensured by construction.

Bibtex

@inproceedings{morreale2021neural,
  title={Neural Surface Maps},
  author={Morreale, Luca and Aigerman, Noam and Kim, Vladimir G and Mitra, Niloy J},
  booktitle={Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition},
  pages={4639--4648},
  year={2021}
}