We present a differentiable function F to composite a set of discrete elements into a pattern image. This directly connects vector graphics to image-based losses (e.g., L_2 loss, style loss) and allows us to optimize discrete elements to minimize losses on the composited image. Minimizing an L_2 loss gives us a decomposition of an existing flat pattern image into a set of depth-ordered discrete elements that can be edited individually. Minimizing a style loss allows us to make a pattern tileable or expand a pattern image into a larger pattern composed of discrete elements.

Abstract

Patterns, which are collections of elements arranged in regular or near-regular arrangements, are an important graphic art form and widely used due to their elegant simplicity and aesthetic appeal. When a pattern is encoded as a flat image without the underlying structure, manually editing the pattern is tedious and challenging as one has to both preserve the individual element shapes and their original relative arrangements. State-of-the-art deep learning frameworks that operate at the pixel level are unsuitable for manipulating such patterns. Specifically, these methods can easily disturb the shapes of the individual elements or their arrangement, and thus fail to preserve the latent structures of the input patterns. We present a novel differentiable compositing operator using pattern elements and use it to discover structures, in the form of a layered representation of graphical objects, directly from raw pattern images. This operator allows us to adapt current deep learning based image methods to effectively handle patterns. We evaluate our method on a range of patterns and demonstrate superiority in the context of pattern manipulations when compared against state-of-the-art pixel-based pixel- or point-based alternatives.

Inverse Pattern decompositions Results

Given the flat pattern images and the elements in the top row, we optimize for elements that reconstruct the pattern image using our differentiable compositing function. The result of the continuous optimization is shown in the second row, and the discretized result (inferred layering information is not shown here) in the third row. In the last row, we show the $L_2$ error between the discretized result and the input image for colors in [0,1]^3. The majority of the errors are evident near the boundaries due to small position inaccuracies of the elements.

Generating mosaics

By decomposing a non-pattern image and adding a loss that penalizes overlaps between elements, we can create mosaics. Here we create a mosaic of the Siggraph Asia logo.

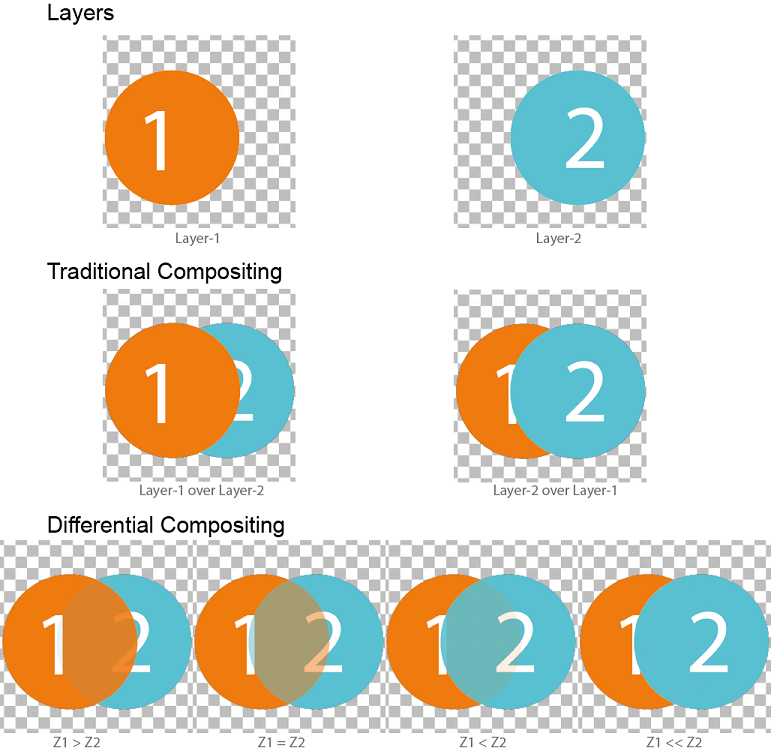
Simple Illustration of Differentiable Compositing

This is a simple Illustration of our proposed compositing function, you can find the numpy code for 2 layer soft compositing function here

Bibtex

@article{reddy2020discovering,
  title={Discovering pattern structure using differentiable compositing},
  author={Reddy, Pradyumna and Guerrero, Paul and Fisher, Matt and Li, Wilmot and Mitra, Niloy J},
  journal={ACM Transactions on Graphics (TOG)},
  volume={39},
  number={6},
  pages={1--15},
  year={2020},
  publisher={ACM New York, NY, USA}
}
			

Acknowledgements

We would like to thank the anonymous reviewers for their helpful suggestions and Maks Ovsjanikov for discussions in an early phase of this project. This research was supported by an ERC Grant (SmartGeometry 335373), Google Faculty Award, and gifts from Adobe.