Super4PCS: Fast Global Pointcloud Registration via Smart Indexing
- Nicolas Mellado1
- Dror Aiger2
- Niloy J. Mitra1
1University College London, 2Google Inc.
12th Symposium on Geometry Processing (2014)

Figure 1: We present Super4PCS, an optimal linear time output-sensitive global alignment algorithm that registers a pair of raw pointclouds in arbitrary initial poses. This example is particularly challenging as no distinctive geometric features are available (see right inset) and color cues (not used) are confusing due to object shininess. Super4PCS works even with low overlap (∼25%), and 20% outlier margin. Results are shown without ICP refinement. The proposed method has linear complexity over the state-of-the-art 4PCS, which has a quadratic time complexity.
Abstract
Data acquisition in large-scale scenes regularly involves accumulating information across multiple scans. A common approach is to locally align scan pairs using Iterative Closest Point (ICP) algorithm (or its variants), but requires static scenes and small motion between scan pairs. This prevents accumulating data across multiple scan sessions and/or different acquisition modalities (e.g., stereo, depth scans). Alternatively, one can use a global registration algorithm allowing scans to be in arbitrary initial poses. The state-of-the-art global registration algorithm, 4PCS, however has a quadratic time complexity in the number of data points. This vastly limits its applicability to acquisition of large environments. We present Super4PCS for global pointcloud registrationthat is optimal, i.e., runs in linear time (in the number of data points) and is also output sensitive in the complexity of the alignment problem based on the (unknown) overlap across scan pairs. Technically, we map the algorithm as an ‘instance problem’ and solve it efficiently using a smart indexing data organization. The algorithm is simple, memory-efficient, and fast. We demonstrate that Super4PCS results in significant speedup over alternative approaches and allows unstructured efficient acquisition of scenes at scales previously not possible.
We propose Super4PCS, a fast global registration for pointsets, which runs in optimal linear time and is output sensitive. The key insight is to remove the quadratic complexity in the original 4PCS algorithm by using an efficient yet practical data structure to solve the core instance problem, i.e., finding all point pairs that are within a distance range (r - ε, r + ε). Specifically, Super4PCS runs in O(n + k1 + k2 ) time where k1 is the number of pairs in Q at a given distance r and k2 is the number of congruent sets. The proposed datastructure naturally extends to higher dimensions and allows a unified treatment of spatial and angular proximity queries. Hence, when auxiliary local surface information (e.g., normals, color) are available, then Super4PCS can directly integrate the information. The proposed construction is adaptive and can be efficiently constructed at run-time with very low memory overheard.
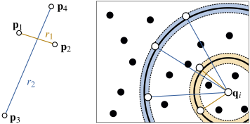 |
Left: Example of a basis in P (for sake of simplicity we show only the distances defined by one pair). Right: For any point qi ∈ Q, pairs are generated by finding the other points close to the hyperspheres centered in qi and with radius r1 ± ε and r2 ± ε. |
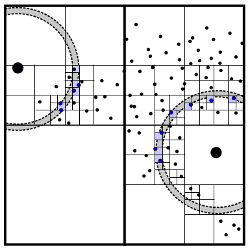 |
Illustration of the simultaneous rasterization of two hyper-spheres of thickness ε and the extraction of points for pairing (in blue), using our procedure. The size of the final cells is equal to ε. Note that in 3D cells get split into 8 cells. |
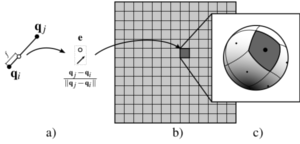 |
Structure used to hash pairs first by their position in the ambient space, and then by their orientation. a) Starting from a pair and its invariant f , we compute a new point e and the pair direction, represented as a normalized vector. b) The position e is used to access cells in a regular grid. c) The orientation is then hashed and the index of the pair is stored in orientation space. |
Bibtex
@article {CGF:CGF12446,
author = {Mellado, Nicolas and Aiger, Dror and Mitra, Niloy J.},
title = {Super 4PCS Fast Global Pointcloud Registration via Smart Indexing},
journal = {Computer Graphics Forum},
volume = {33},
number = {5},
issn = {1467-8659},
url = {http://dx.doi.org/10.1111/cgf.12446},
doi = {10.1111/cgf.12446},
pages = {205--215},
year = {2014},
}
Erratum
There was an error in the original paper (Figure 9: wrong hashing formula, inconsistent with inline description). We apologize for any inconvenience this may have caused.
Corrected versions can be downloaded below.