Designing Chain Reaction Contraptions from Causal Graphs
- Robin Roussel1,2
- Marie-Paule Cani2
- Jean-Claude Léon3
- Niloy J. Mitra1
1University College London 2LIX, École Polytechnique 3Grenoble Alpes University, CNRS, Inria, Grenoble INP, LJK
SIGGRAPH 2019
Invited for Oral presentation at VIS 2019
Abstract
Chain reaction contraptions, commonly referred to as Rube Goldberg machines, achieve simple tasks in an intentionally complex fashion via a cascading sequence of events. They are fun, engaging and satisfying to watch. Physically realizing them, however, involves hours or even days of manual trial-and-error effort. The main difficulties lie in predicting failure factors over long chains of events and robustly enforcing an expected causality between parallel chains, especially under perturbations of the layout. We present a computational framework to help design the layout of such contraptions by optimizing their robustness to possible assembly errors. Inspired by the active learning paradigm in machine learning, we propose a generic sampling-based method to progressively approximate the success probability distribution of a given scenario over the design space of possible scene layouts. The success or failure of any given simulation is determined from a user-specified causal graph enforcing a time ordering between expected events. Our method scales to complex causal graphs and high dimensional design spaces by dividing the graph and scene into simpler sub-scenarios. The aggregated success probability distribution is subsequently used to optimize the entire layout. We demonstrate the use of our framework through a range of real world examples of increasing complexity, and report significant improvements over alternative approaches.
This project appeared in the French newspaper Le Monde.
Video
Method
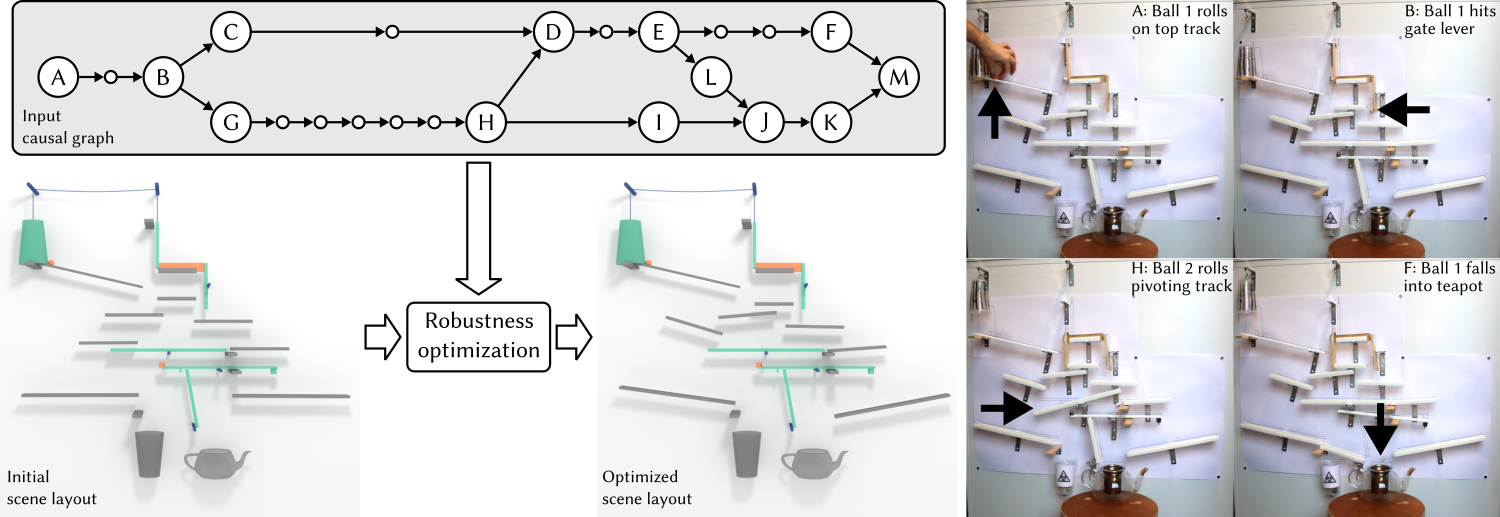
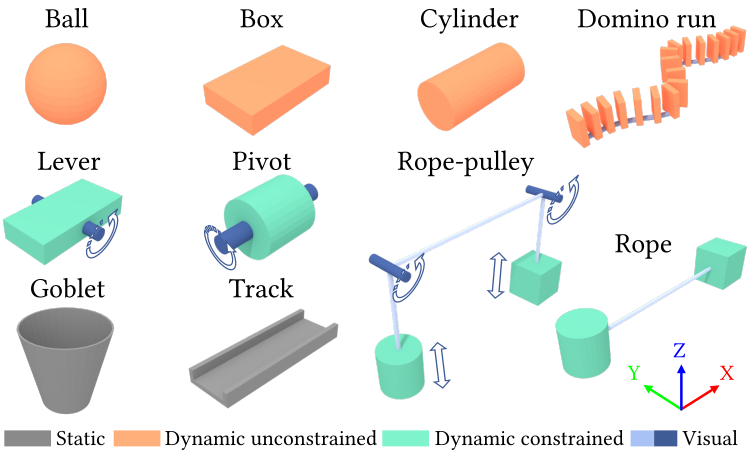
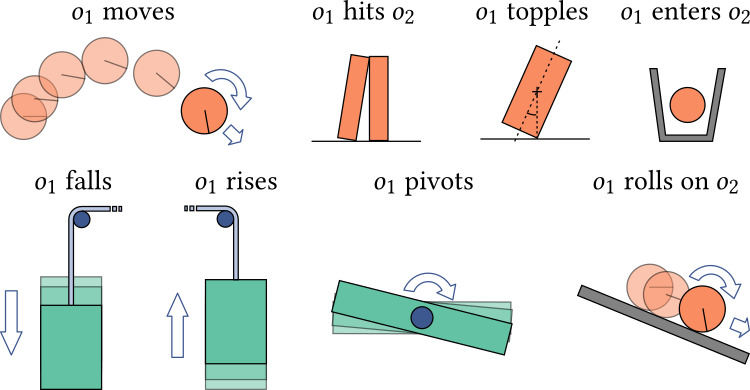
Our system provides a number of primitives (left) and associated events (right) to easily define scenes and causal graphs.
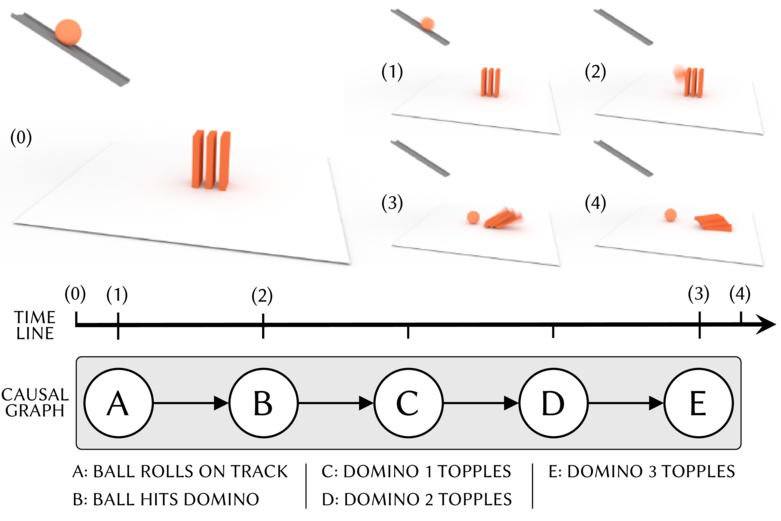
Together, a scene, a causal graph and a parametric domain constitute a scenario: for instance, in the figure above, a ball initially at rest on a track starts rolling and falls onto a domino runs, which topples.
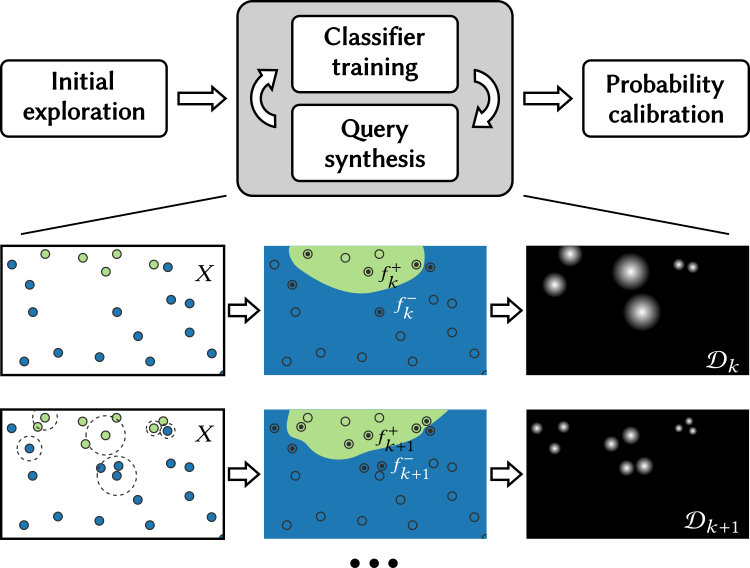
Our goal is to build a success probability distribution in the design space of the contraption, where each point corresponds to a different layout (as shown on the left: higher value means higher probability). To achieve this, we first efficiently search for successful points in the design space by running simulations (see right). Then, we train a classifier on this dataset to predict the success or failure of any point in this design space. We use active learning to augment the dataset and improve the classification accuracy. Lastly, we calibrate the classification score to obtain a probability of success given the layout.
Results
The following scenarios were all designed using our system, and were successfully reproduced in real life (see video).
BallRun: In this scenario, the small orange plank needs to fall quickly enough so that the ball can enter the goblet.
CausalitySwitch: Here, whichever side is fastest closes the path of the other. Changing the causal graph's last event allows us to select the ending (both endings are shown in the video).
LongChain: This long chain of events contains challenging parts, such as the orange plank on the left falling through a narrow opening into a goblet.
TeapotAdventure: In this scenario, two balls need to open each other's path in order to end up together in the teapot. The causal graph contains several difficult synchronizations.

We define three baselines to quantitatively evaluate our method. Please refer to the paper for details.
Bibtex
@article{RousselEtAl:CausalGraphs:SIGGRAPH2019,
title = {Designing Chain Reaction Contraptions from Causal Graphs},
author = {Roussel, Robin and Cani, Marie-Paule and L{\'e}on, Jean-Claude and Mitra, Niloy J.},
year = {2019},
journal = {ACM Trans. Graph.},
volume = {38},
number = {4},
pages = {43:1--43:13},
doi = {10.1145/3306346.3322977},
}
Acknowledgements
We are grateful to the reviewers for their helpful feedback. We thank Dan Koschier for proofreading the paper, Tobias Ritschel and Simon Julier for their valuable comments and Mohamed Sayed for the video voiceover. This work was funded by an ERC Starting Grant (SmartGeometry StG-2013-335373), an ERC PoC Grant (SemanticCity), a Google Faculty Award, a Royal Society Advanced Newton Fellowship and gifts from Adobe.