
For modelling the 3D reconstructed grids, we use the ReLU-Fields representation instead of a standard RGBA volumetric grid, for inherently inducing the notion of free space in the 3D-grid. Given a user-provided AABB (Axis-Aligned Bounding Box), we represent the RGB+A signal inside it using a volumetric grid \(\mathcal{V}\) of fixed resolution \(nv_x \times nv_y \times nv_z\). The \(A\) channel of the grid stores feature values in the range \([-1, 1]\) and the \(RGB\) channels store the normal colour values in the range \([0, 1]\). The values on the grid are trilinearly interpolated to obtain continuous fields, with the addition of applying a \(ReLU\) non-linearity after interpolating the values on the \(A\) grid.
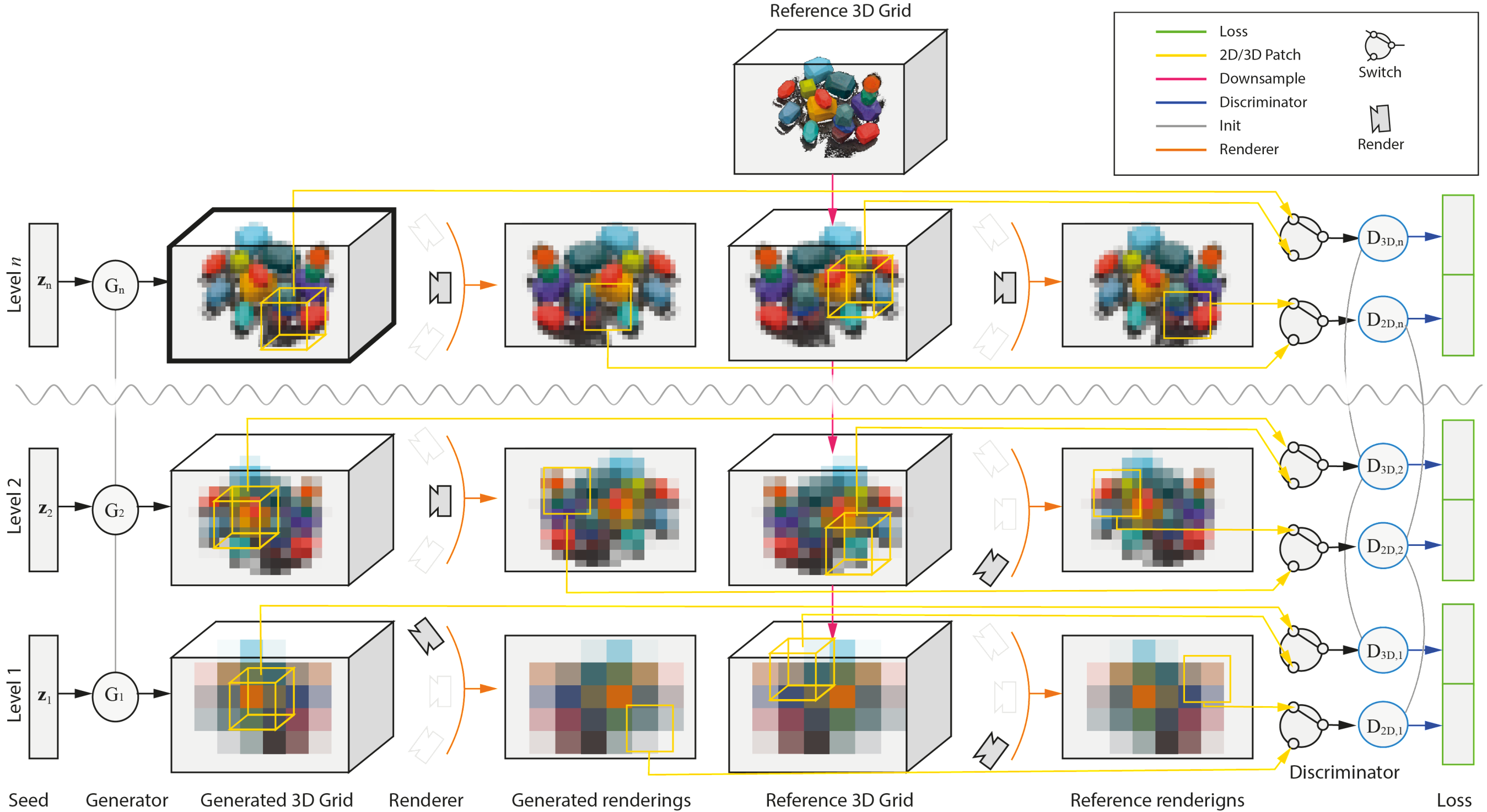
Training the generative model makes use of the 3D feature grid \(\mathcal{V}\) trained in the previous section, which we denote as the reference grid. The following subsections provide details about the Generator architecture, followed by the multi-scale generative training, and the adversarial losses used.
Generator: The generator network \(G\) maps the random spatial grids of latent codes \(z\) to a 3D feature grid \(G(z)\) at the coarsest stage. While it adds fine residual details to the previous stage's outputs for the rest of the stages similar to SinGAN. The latent codes at the coarsest stage \(z_0\) are \(seedDimension=4\) dimensional while correspond to a blend between previous Stage's output and random noise for subsequent stages. I.e. \(z_t = G_{t-1}(z_{t-1}) + \epsilon\), where, \( \epsilon \in \mathbb{R}^{h_t \times w_t \times d_t} \) and \(\epsilon \sim \mathbb{N}(0, I)\).
Training: We train the architecture progressively: the generator first produces grids of reduced resolution. Only once this has converged, layers are added and the model is trained to produce the higher resolution. Note that we freeze the previously trained layers in order to avoid the GAN training from diverging. We employ an additional reconstruction loss that enforces one single fixed seed \(z*\) to map to the reference grid. We supervise this fixed seed loss via an MSE over the 3D grids and with 2D rendered patches.
3D discriminator: The 3D discriminator compares 3D patches from the generated grid to 3D patches of the reference grid. Let \(P_{3D}(\mathcal{V})\) be the operator that extracts a random patch from the 3D grid \(\mathcal{V}\). Thus the distributions that the 3D discriminator tries to discriminate are, \(p^{3D}_F = P_{3D}(G(z))\) and \(p^{3D}_{R} = P_{3D}(\mathcal{V})\).
2D discriminator: A 2D discriminator discriminates between 2D patches of the rendered views of the generated grid and the 2D patches obtained from the rendered views of the reference grid \(\mathcal{V}\). To render the 3D grids we need to model another distribution of the poses, which we denote as \(\mathcal{D}\), that we uniformly sample from a top-hemisphere around the grid. The focal lengths of the cameras are interpolated linearly for the various stages such that the value at the final stage corresponds to the actual camera intrinsics. Further, let \(P_{2D}()\) be an operator to extract a random patch from a 2D image. Thus, the 2D discriminator works upon the distributions: \(p^{2D}_F = P_{2D}(R(G(z), \mathcal{D}))\) and \(p^{2D}_R = P_2D(R(\mathcal{V}, \mathcal{D}))\). Where, the \(R()\) corresponds to the rendering function, for which we use the differentiable EmissionAbsorption model.
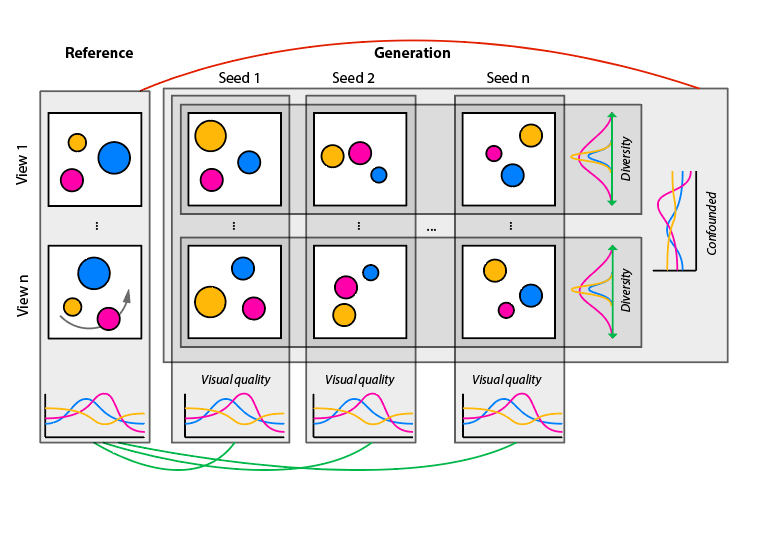
Quality: Visual quality is measured as the expectation of SIFID (Single Image FID) scores between the distribution of exemplar 2D images and the distribution of rendered generated 2D images for a fixed camera over multiple seeds. We compute this expectation by taking a mean over a number of camera-views. This is similar in spirit to SIFID, except we compute it over images rendered from different views of the 3D scenes. Lower distance reflects better quality.
Diversity: Unfortunately, in the single scene case, we cannot meaningfully compute FID scores between the exemplar patch distribution and the distribution of all generated patches across seeds as it would make diversity appear as a distribution error. This is different from a typical GAN setup where we are given real images as samplings of desirable distribution of both quality and diversity. Instead, we measure scene diversity as the variance of a fixed patch from a fixed view over random seeds, which is a technique used to study texture synthesis diversity. Larger diversity is better.
Our Quality v/s Diversity results. A good single scene generative model needs to have a good mix of quality and diversity – excellent quality with no diversity or vice versa are both undesirable. Visual Quality and Scene Diversity for different methods (columns) and different data sets (rows). To simplify comparison, we normalize the numbers so that ours is always 1. The best for each metric on each dataset is bolded and second best is underlined. Please refer to the supplementary for unscaled numbers.
GT
Seed 1
Seed 2
Seed 3
GT
Seed 1
Seed 2
Seed 3
GT
Seed 1
Seed 2
Seed 3
GT
Seed 1
Seed 2
Seed 3
GT
Seed 1
Seed 2
Seed 3
GT
Seed 1
Seed 2
Seed 3
GT
Seed 1
Seed 2
Seed 3
GT
Seed 1
Seed 2
Seed 3
@inproceedings{
karnewar_3InGan_3dv_22,
author = {Karnewar, Animesh and Ritschel, Tobias and Wang, Oliver and Mitra, Niloy},
title = {{3inGAN}: Learning a {3D} Generative Model from Images of a Self-similar Scene},
year = {2022},
booktitle = {Proc. {3D} Vision ({3DV})}
}

The research was partially supported by the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 956585, gifts from Adobe, and the UCL AI Centre.