SMASH: Physics-guided Reconstruction of Collisions from Videos
- Aron Monszpart1
- Nils Thuerey2
- Niloy J. Mitra1
1University College London 2Technical University of Munich
SIGGRAPH Asia 2016

Starting from an input video of a collision sequence behind a curtain (top), SMASH reconstructs an accurate physically valid collision (bottom) using laws of rigid body physics for regularization. Note the reconstructed spin (i.e., angular velocity) of the objects.
Abstract
Collision sequences are commonly used in games and entertainment to add drama and excitement. Authoring even two body collisions in the real world can be difficult, as one has to get timing and the object trajectories to be correctly synchronized. After tedious trial-and-error iterations, when objects can actually be made to collide, then they are difficult to capture in 3D. In contrast, synthetically generating plausible collisions is difficult as it requires adjusting different collision parameters (e.g., object mass ratio, coefficient of restitution, etc.) and appropriate initial parameters. We present SMASH to directly read off appropriate collision parameters directly from raw input video recordings. Technically we enable this by utilizing laws of rigid body collision to regularize the problem of lifting 2D trajectories to a physically valid 3D reconstruction of the collision. The reconstructed sequences can then be modified and combined to easily author novel and plausible collisions. We evaluate our system on a range of synthetic scenes and demonstrate the effectiveness of our method by accurately reconstructing several complex real world collision events.
Reconstruction of collisions

We tested our algorithm on multiple collision sequences. Here we show a selection of frames of input frames and corresponding reconstructed frames. Please refer to the supplementary video.
Initialization to reconstruction of the collision

a) the result of our initialization: labeled centroid and approximate depth values (green dots) together with the initialized orientations (green cuboids); b) 3D parabolas resulting from our full optimization (red curves), and c) motion over time (colored cuboids).
Compact modeling
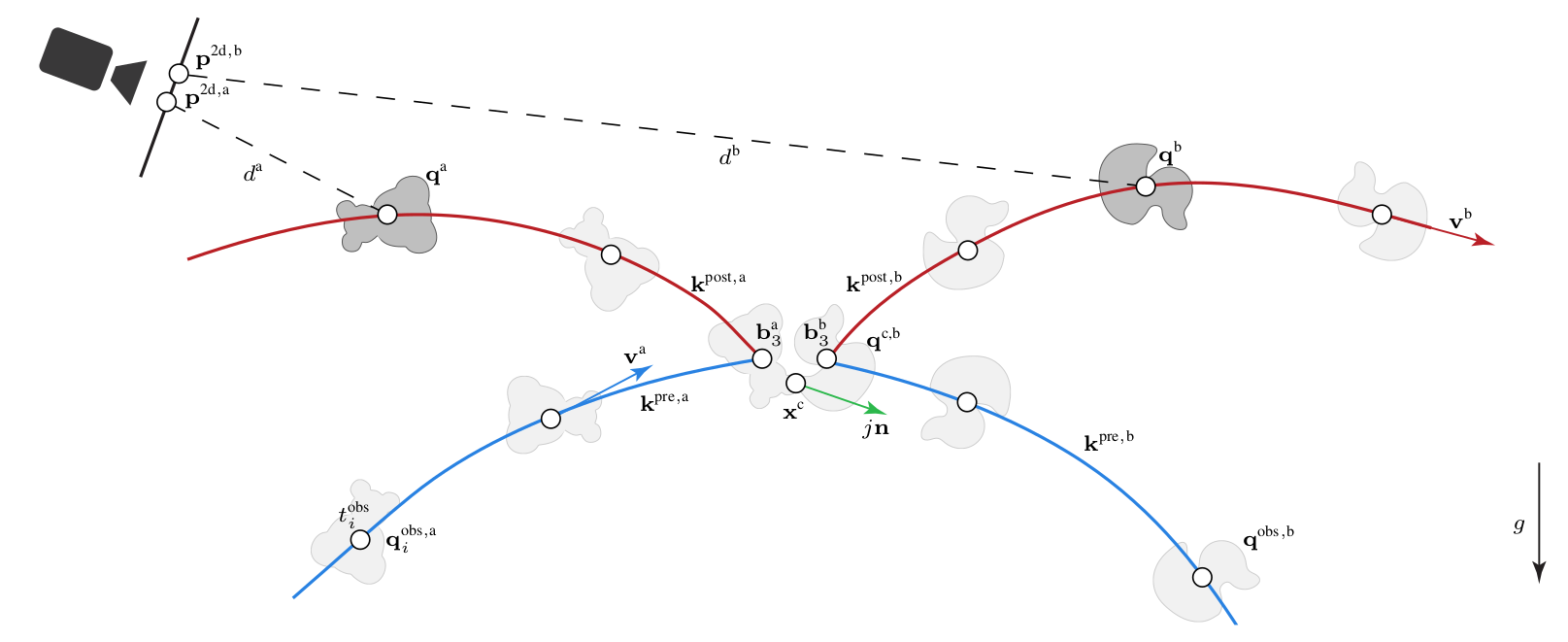
Modeling two body collisions: We extract dense position estimates from a video input, and augment it with sparse semi-automatically generated orientations. These observations are linked with laws of physics: the individual trajectories should be parabolas as we assume the bodies to have ballistic motion, and they get coupled at the (unknown) collision point based on conservation laws.
Real evaluation
Various c estimates obtained by our method as compared against c_m obtained using alternate potential energy-based estimation, which is valid only when the object has no angular momentum. All the examples are instances of collision of a single object against an infinite mass object (i.e., carpeted ground).
Synthetic evaluation

Synthetic evaluation of robustness towards noise in the orientations. Gap (2, 4, 6, 8, 10) denotes the distance in time to the closest orientation around collision time. Dashed lines denote ground truth, coefficient of restitution = 0.49 and mass ratio = 1.33.
Evaluation of terms (synthetic)
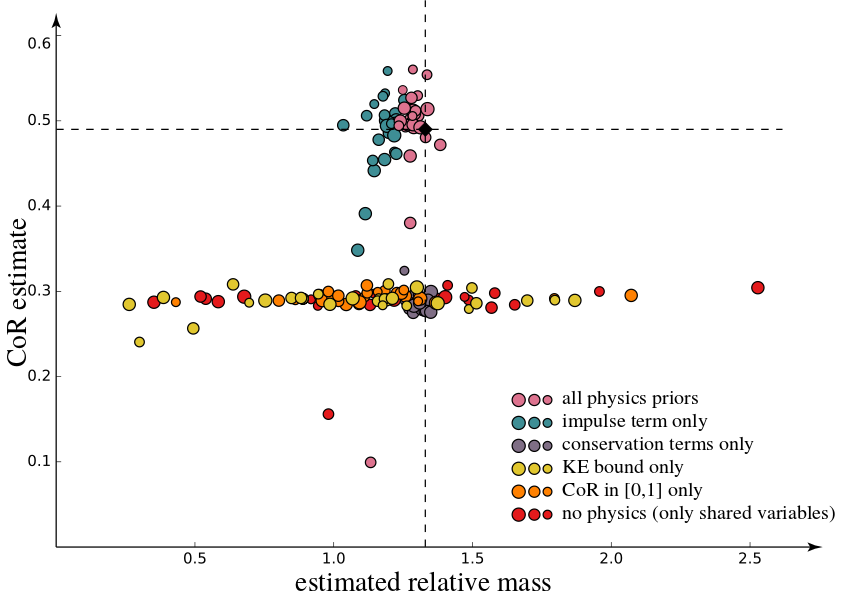
Evaluation of the role of different terms. Impulse-based physics coupling is clearly the essential ingredient, while the other terms act as secondary regularizer. Larger circles show experiments with larger noise (positions and orientations). The input was a noise-free run of our automatic parabola initialization and synthetic orientations at least five timesteps away from collision time. Dashed lines denote ground truth, coefficient of restitution = 0.49 and mass ratio = 1.33.
Bibtex
@article{MonszpartThuereyMitra:SMASH:2016,
author = {Monszpart, Aron and Thuerey, Nils and Mitra, Niloy J.},
title = {{SMASH: Physics-guided Reconstruction of Collisions from Videos}},
year = {2016},
month = {nov},
journal = {{ACM} Trans. Graph. ({SIGGRAPH} Asia)},
volume = {35},
number = {6},
pages = {199:1--199:14},
articleno = {199},
publisher = {{ACM}
}
Acknowledgements
We thank our reviewers for their invaluable comments. We also thank Gabriel Brostow, Paul Guerrero, Martin
Kilian, Oisin Mac Aodha, Moos Hueting, James Hennessey, Stephan Garbin, Chris Russell, Clément Godard, Peter Hedman and Veronika Benis
for their help, comments and ideas. This work was partially funded by the ERC Starting Grant SmartGeometry (StG-2013-335373),
the ERC Starting Grant realFlow (StG-2015-637014), UCL Impact, a Google PhD Fellowship, and gifts by Adobe.








