String Actuated Curved Folded Surfaces
- Martin Kilian1,2
- Aron Monszpart1
- Niloy J. Mitra1
1University College London 2Vienna University of Technology
ACM Transactions on Graphics 2017

The top row shows a crease pattern together with the strings S = {a, b, c, d, e} computed by our algorithm and simulation of the induced, string driven folding motion. The bottom row shows a physical realization of the same crease pattern as a thin aluminum sheet. Each string is realized as a strand of colored thread. Strings are collected at a single anchor point and folding is driven by pulling the threads.
Abstract
Curved folded surfaces, given their ability to produce elegant freeform shapes by folding flat sheets etched with curved creases, hold a special place in computational Origami. Artists and designers have proposed a wide variety of different fold patterns to create a range of interesting surfaces. The creative process, design as well as fabrication, is usually only concerned with the static surface that emerges once folding has completed. Folding such patterns, however, is difficult as multiple creases have to be folded simultaneously to obtain a properly folded target shape. We introduce string actuated curved folded surfaces that can be shaped by pulling a network of strings thus vastly simplifying the process of creating such surfaces and making the folding motion an integral part of the design. Technically, we solve the problem of which surface points to string together and how to actuate them by locally expressing a desired folding path in the space of isometric shape deformations in terms of novel string actuation modes. We demonstrate the validity of our approach by computing string actuation networks for a range of well known crease patterns and testing their effectiveness on physical prototypes. All the examples in this paper can be downloaded for personal use (link).
String actuated folding
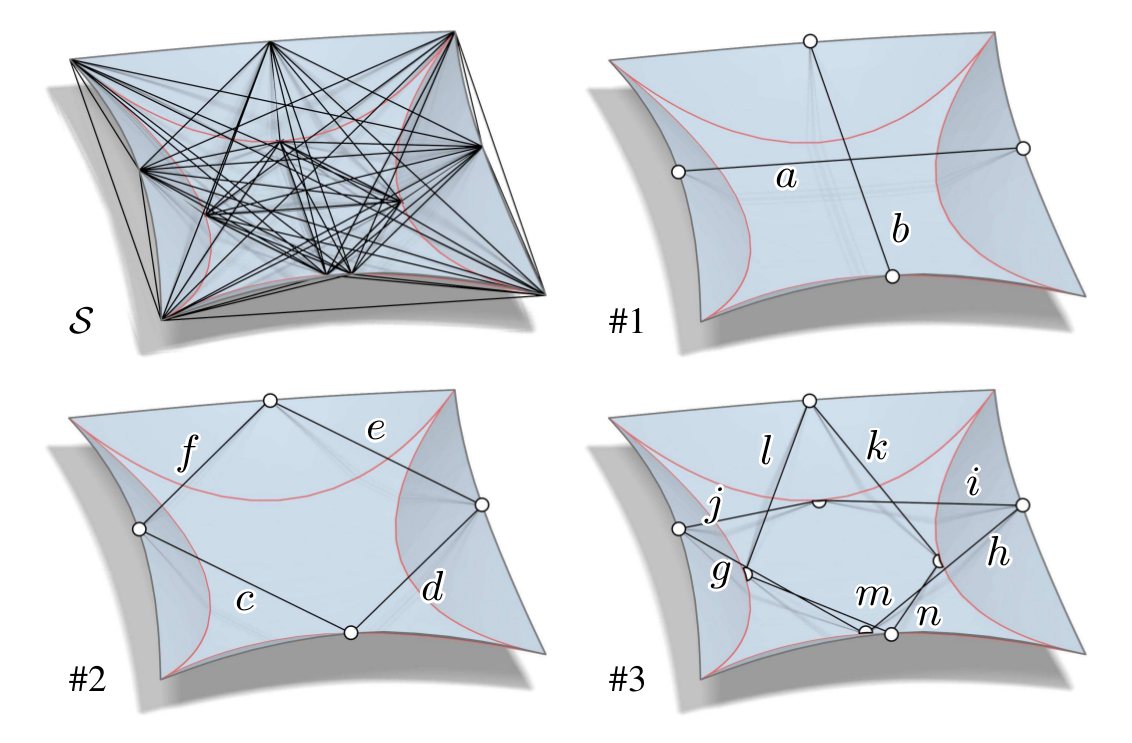
Input strings S to global optimization (top left) and three solutions obtained by iteratively removing a discovered solution S_∗ from S and then rerunning the optimization.
Rigging a crease pattern. Holes are punched at actuation point locations. All threads are collected at an anchor point (hole in the plexiglass pane). Actuation point locations may be reinforced with metal eyelets as shown.
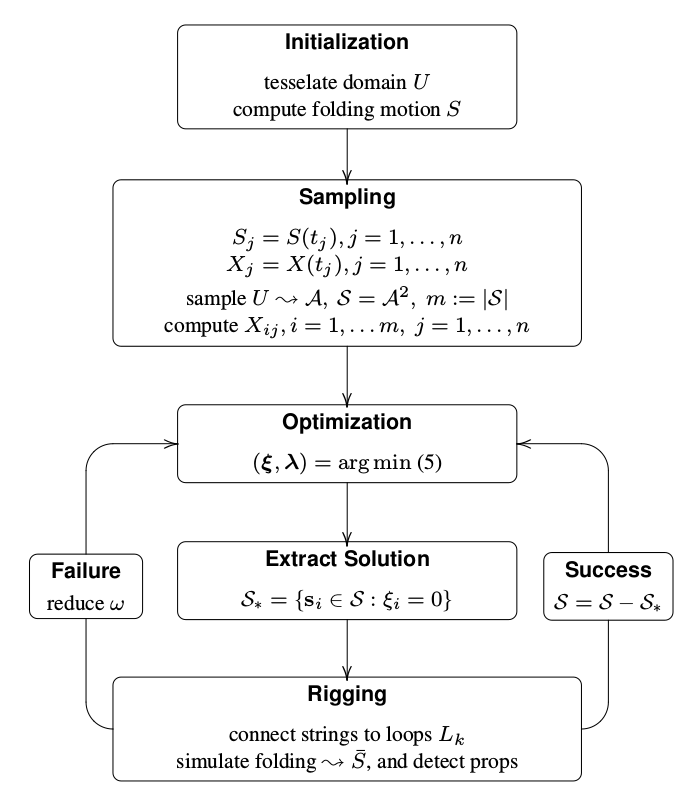
Main steps to compute a stringing that drives the folding of a planar sheet according to a given crease pattern. The optimization loop terminates once a given number of solutions is extracted or after repeated failure.
Results
Concept chair
The top row shows the result of simulated string actuated folding employing a length constraint on strings c and g. We realized those length constraints by enclosing the corresponding thread segments in plastic tubes of the appropriate length. The folding result without props is shown below, third row, right.
Initial string graph S for the Concept chair model and two solutions. Starting from the left, the second row shows the target shape and the simulated string driven folding results using #1 and #2, respectively. Actual folding results confirm the simulation (third row). The fourth row shows final folding results and how props are used for the stringing of #1 and #2.
Apricot
Folding the Apricot. The target deformation is shown in the top row. String acuated folding (bottom row) employs solutions #1 and #3 as shown in the top right images below. The two nylon threads are pulled downwards through a hole in the tabletop.
Initial string graph (top left) and three solutions. In all cases the stringing is given as {a, b, c, d, e}. The top right shows the rigged CP and the partially folded CP viewed from below. The last row shows the different planes in which the strings of solution #1 and #3 move during folding.
Nautilus
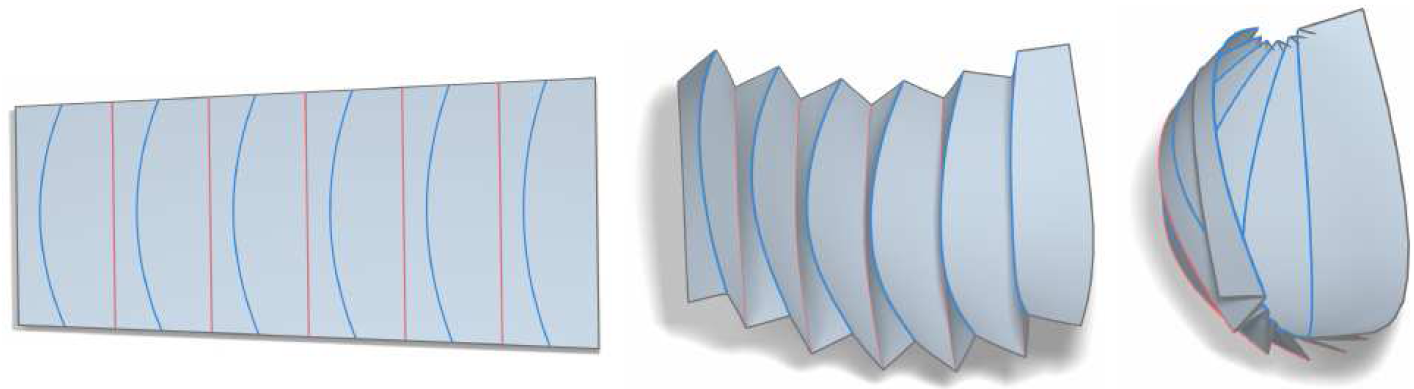
Target deformation of the Nautilus CP (top row) and string driven folding motion induced by extending solution #2 of a 6 segment section to the complete pattern consisting of 15 segments. The paper model is made from 5 sheets of A3 drawing paper. Each sheet holds 3 segments, sheets are joined along the boundary mountain folds using masking tape (yellow).
Target folding motion for a 6 segment section of the Nautilus crease pattern. The bottom row shows a rigged paper model of the pattern.
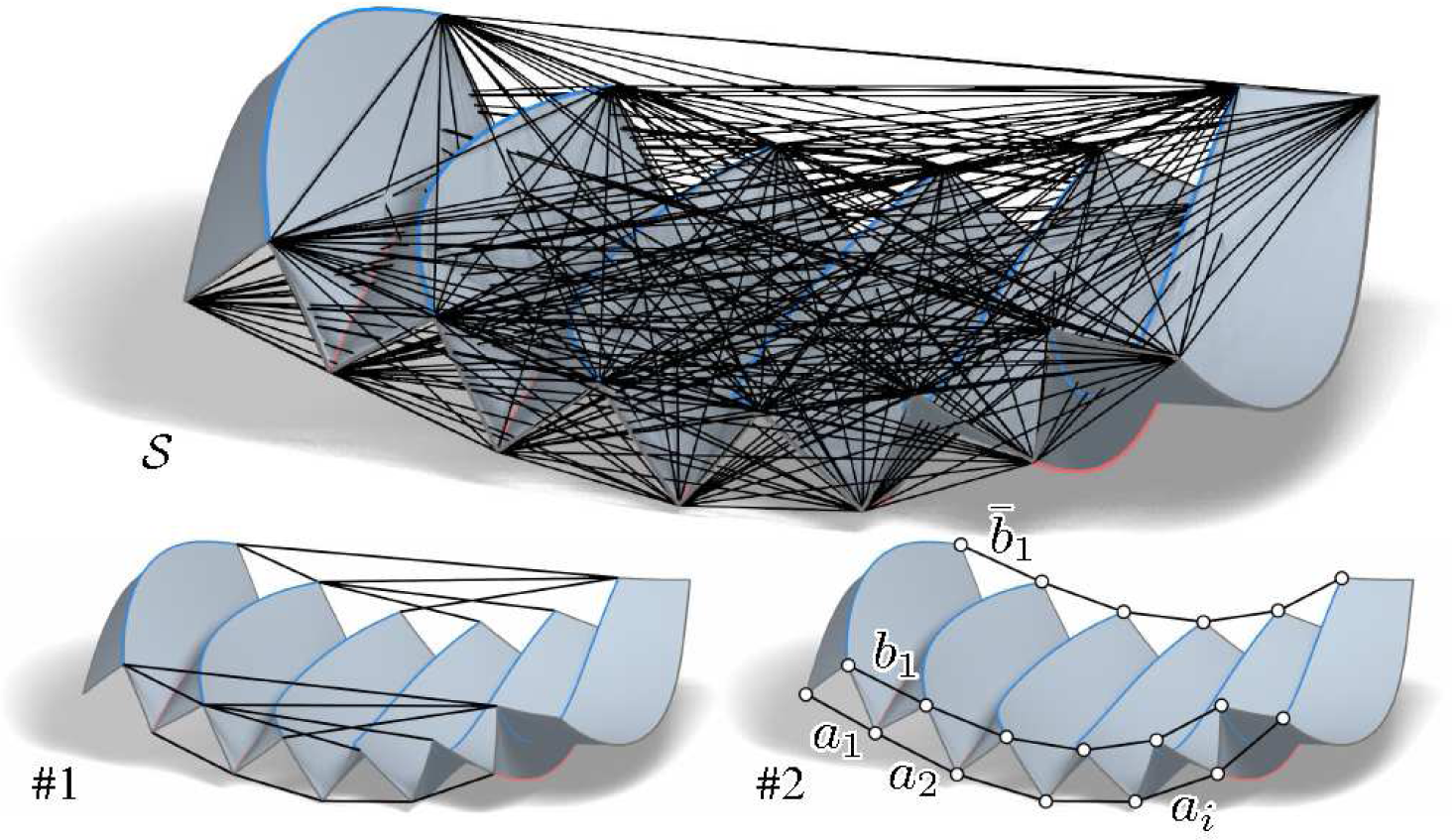
Initial set S of strings for the Nautilus CP and the computed solutions. Please refer to the text for details.
Bibtex
@article{StringActuated:KilianMonszpartMitra:TOG:2017,
title = {String Actuated Curved Folded Surfaces},
author = {Martin Kilian and Aron Monszpart and Niloy J. Mitra},
year = {2017},
journal = {{ACM} Transactions on Graphics},
volume = {36},
number = {3},
month = May,
year = {2017},
issn = {0730-0301},
pages = {25:1--25:13},
articleno = {25},
numpages = {13},
url = {http://doi.acm.org/10.1145/3015460},
doi = {10.1145/3015460},
acmid = {3015460},
publisher = {ACM}
}
Acknowledgements
Martin Kilian was supported by the Erwin Schrödinger fellowship J-3678-N25 awarded by the Austrian Science Fund (FWF), ERC StG-2013-335373, and the DFG-Collaborative Research Center, TRR 109, ‘Discretization in Geometry and Dynamics’ through grant I-706-N26 of FWF. Aron Monszpart was supported by a Google PhD Fellowship, the ERC Starting Grant SmartGeometry (StG-2013-335373), and Adobe Research. We also thank the Institute of Making for providing us with the equipment and expert advise to manufacture the prototypes.